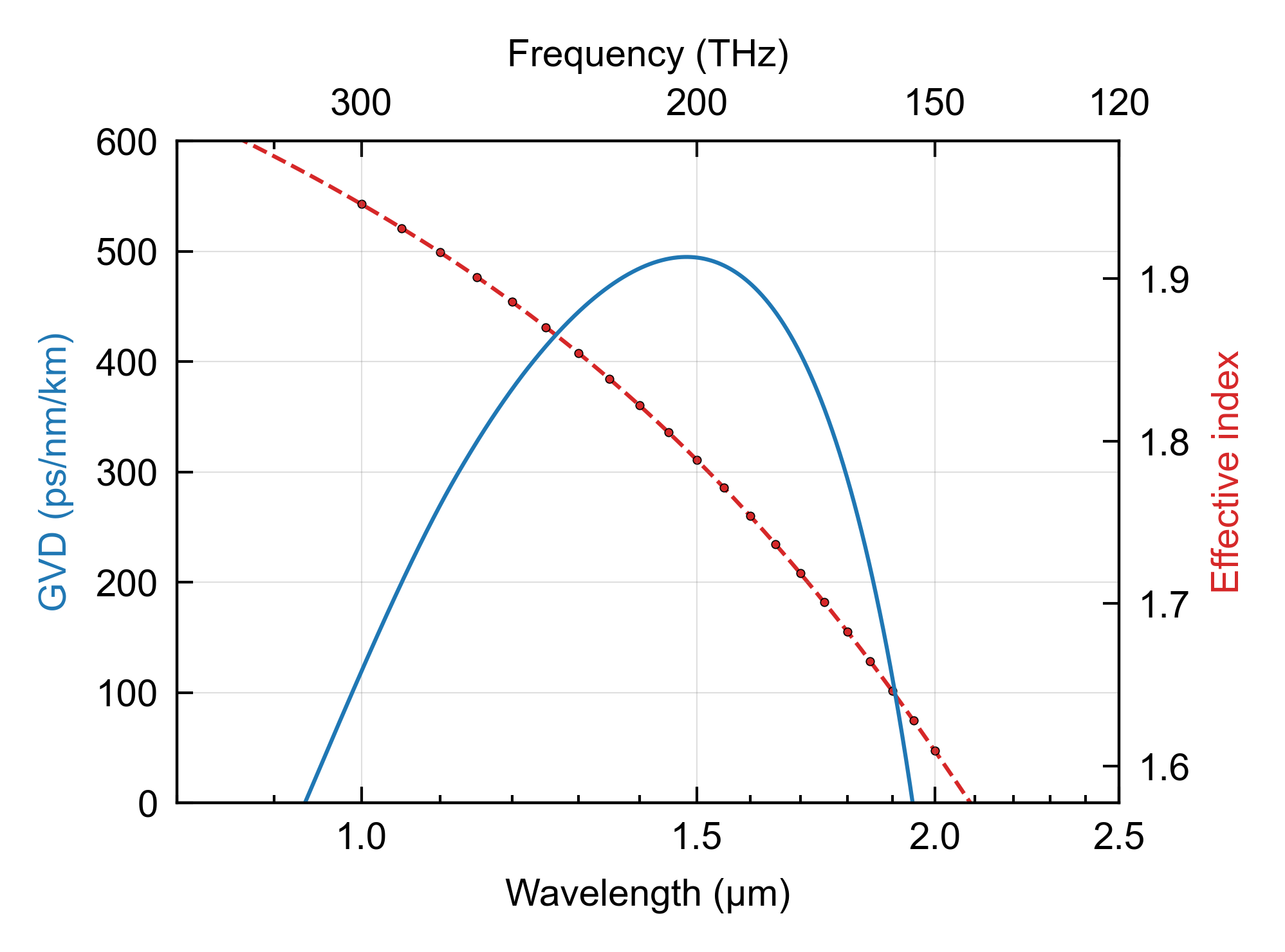
Dispersion Sweep
The sweep function is demonstrated to calculate dispersion of a waveguide. See for a comparison: J. A. Black, R. Streater, K. F. Lamee, D. R. Carlson, S.-P. Yu, and S. B. Papp, “Group-velocity-dispersion engineering of tantala integrated photonics,” Opt. Lett. 46, 817 (2021).
This code example is licensed under the BSD 3-Clause License.
import emodeconnection as emc
import numpy as np
## Set simulation parameters
dx, dy = 10, 10 # [nm] resolution
h_core = 750 # [nm] waveguide core height
b_clad = 2500 # [nm] waveguide top and bottom clad
h_clad = 1500 # [nm] waveguide top and bottom clad
w_core = h_core*1.25 # [nm] waveguide core width
w_trench = 2500 # [nm] waveguide side trench width
num_modes = 1 # [-] number of modes
boundary = 'TE'
wav_nm_ = np.arange(1000, 2001, 50) # [nm]
## Connect and initialize EMode
em = emc.EMode(simulation_name = 'dispersion')
## Settings
em.settings(
x_resolution = dx, y_resolution = dy,
window_width = w_core + w_trench*2,
window_height = h_core + b_clad + h_clad,
num_modes = num_modes, boundary_condition = boundary,
background_refractive_index = 'Air')
## Draw shapes
em.shape(name = 'BOX', refractive_index = 'SiO2', height = b_clad)
em.shape(name = 'core', refractive_index = 'Ta2O5', width = w_core, height = h_core)
## Run wavelength sweep
data = em.sweep(key='wavelength', values = wav_nm_,
result = ['effective_index'])
## Close EMode
em.close()
%% Set simulation parameters
dx = 10; dy = 10; % [nm] resolution
h_core = 750; % [nm] waveguide core height
b_clad = 2500; % [nm] waveguide top and bottom clad
h_clad = 1500; % [nm] waveguide top and bottom clad
w_core = h_core*1.25; % [nm] waveguide core width
w_trench = 2500; % [nm] waveguide side trench width
num_modes = 1; % [-] number of modes
boundary = 'TE';
wav_nm_ = 1000:50:2000; % [nm]
%% Connect and initialize EMode
em = emodeconnection_debug('simulation_name', 'dispersion');
%% Settings
em.settings( ...
'x_resolution', dx, 'y_resolution', dy, ...
'window_width', w_core + w_trench*2, ...
'window_height', h_core + b_clad + h_clad, ...
'num_modes', num_modes, 'boundary_condition', boundary, ...
'background_refractive_index', 'Air');
%% Draw shapes
em.shape('name', 'BOX', 'refractive_index', 'SiO2', 'height', b_clad);
em.shape('name', 'core', 'refractive_index', 'Ta2O5', 'width', w_core, ...
'height', h_core);
%% Run wavelength sweep
data = em.sweep('key', 'wavelength', 'values', wav_nm_, ...
'result', ['effective_index']);
%% Close EMode
em.close();
Console output:
EMode 0.1.0 - email
Sweeping setting parameter 'wavelength'... completed in 52.8 sec
Exited EMode
A separate script can be used to plot the results.
import emodeconnection as emc
import numpy as np
from scipy.interpolate import UnivariateSpline
## Extract sweep results without an EMode license
data = emc.get(variable = 'sweep_data',
simulation_name = 'dispersion')
## Calculate dispersion
ind = np.argsort(data['values'])
n_eff_spl = UnivariateSpline(
data['values'][ind], data['effective_index'][ind], s=0, k=4)
n_eff_spl_2d = n_eff_spl.derivative(n = 2)
wav_nm_fit = np.arange(800, 2501, 1) # [nm]
c = 299792458 # [m/s]
D = -wav_nm_fit/c*n_eff_spl_2d(wav_nm_fit)*1e12/1e-3 # [ps/nm/km]
## Plot
import matplotlib.pyplot as plt
from matplotlib import rc as mplrc
fw, LW = 8/2.54, 0.5
mplrc('font',**{'family':'sans-serif','sans-serif':['Arial'],'size':7})
mplrc('axes', linewidth=LW, axisbelow=True)
mplrc('xtick', bottom=True, top=True, direction='in')
mplrc('ytick', left=True, right=True, direction='in')
mplrc('xtick.major', size=3, width=LW)
mplrc('xtick.minor', size=1.5, width=LW)
mplrc('ytick.major', size=3, width=LW)
mplrc('figure',figsize=[fw, fw/2**0.5])
fig, ax = plt.subplots(1, 1)
ax.set_xlabel(u'Wavelength (\u03bcm)')
ax.set_ylabel('GVD (ps/nm/km)', color = 'tab:blue')
ax.axes.set_xscale('log')
ax2 = ax.twinx()
ax2.set_ylabel('Effective index', color = 'tab:red')
ax.grid(visible=True, which='major', axis='both', linewidth=LW/2, color='grey', alpha=0.25)
ax.plot(wav_nm_fit, D,
color = 'tab:blue', marker = '', linestyle = '-',
lw = LW*1.5)
ax2.plot(wav_nm_fit, n_eff_spl(wav_nm_fit),
color = 'tab:red', marker = '', linestyle = '--',
lw = LW*1.5)
ax2.plot(data['values'], data['effective_index'],
color = 'tab:red', marker = 'o', linestyle = '',
ms = 1.5, mec = 'k', mew = 0.2)
ax.set_xlim([800, 2500])
xticks_nm = np.array([1000, 1500, 2000, 2500])
xticks_nm_minor = np.arange(800, 2500.1, 100)
ax.set_xticks(xticks_nm_minor, labels=''*len(xticks_nm_minor), minor=True)
ax.set_xticks(xticks_nm)
ax.set_xticklabels(['%0.1f' % (x*1e-3) for x in xticks_nm])
ax.set_ylim([0, 600])
ax2.set_ylim([
np.min(data['effective_index'])*0.98,
np.max(data['effective_index'])*1.02])
ax3 = ax.twiny()
ax3.axes.set_xscale('log')
ax3.set_xlim(ax.get_xlim())
ax3.set_xlabel('Frequency (THz)')
ax3.set_xticks(xticks_nm)
ax3.set_xticklabels(['%0.0f' % x for x in c/xticks_nm*1e-3])
ax.set_zorder(ax2.get_zorder()+1)
ax.patch.set_visible(False)
fig.savefig('dispersion.png', dpi=600, bbox_inches='tight')
Figures:
